Upravený R-na druhou je upravená verze R-na druhou, která zohledňuje prediktory, které nejsou v regresním modelu významné. Jinými slovy, upravený R-kvadrát ukazuje, zda přidání dalších prediktorů vylepšuje regresní model nebo ne. Abychom pochopili upravený R-kvadrát, je nutné porozumět R-kvadrátu.
Souhrn:
- Upravený R-na druhou je upravená verze R-na druhou, která se upravuje pro prediktory, které nejsou v regresním modelu významné.
- Ve srovnání s modelem s dalšími vstupními proměnnými znamená nižší upravený R-kvadrát, že další vstupní proměnné nepřidávají modelu hodnotu.
- Ve srovnání s modelem s dalšími vstupními proměnnými vyšší upravený R-kvadrát naznačuje, že další vstupní proměnné přidávají modelu hodnotu.
Co je to R-kvadrát?
R-kvadrát, nazývaný také koeficient determinace Koeficient determinace Koeficient determinace (R² nebo r-kvadrát) je statistické měřítko v regresním modelu, které určuje podíl rozptylu v závislé, se používá k vysvětlení stupně do které vstupní proměnné (predikční proměnné) vysvětlují variaci výstupních proměnných (predikovaných proměnných). Pohybuje se od 0 do 1. Například pokud je R-kvadrát 0,9, znamená to, že 90% odchylek ve výstupních proměnných je vysvětleno vstupními proměnnými. Obecně řečeno, vyšší R-kvadrát označuje lepší přizpůsobení modelu. Zvažte následující diagram:
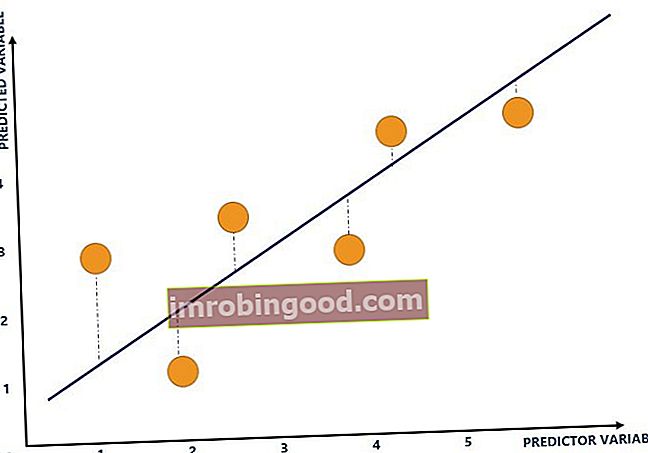
Modrá čára označuje čáru nejvhodnější a ukazuje vztah mezi proměnnými. Úsečka se počítá pomocí regresní analýzy Regresní analýza Regresní analýza je sada statistických metod používaných pro odhad vztahů mezi závislou proměnnou a jednou nebo více nezávislými proměnnými. Lze jej použít k posouzení síly vztahu mezi proměnnými a k modelování budoucího vztahu mezi nimi. a je vyneseno tam, kde jsou minimalizovány svislé vzdálenosti (modré tečkované čáry) žlutých teček od čáry nejvhodnější.
Žluté tečky odkazují na graf vstupních a výstupních proměnných. Vstupní proměnná je vynesena na ose x, zatímco výstupní proměnná je vynesena na ose y. Například výše uvedený graf se skládá z následující datové sady:

Modré tečkované čáry odkazují na vzdálenost grafu vstupních a výstupních proměnných od čáry nejvhodnější. R-kvadrát je odvozen od vzdálenosti všech žlutých bodů od čáry nejvhodnější (modrá čára). Například následující diagram by ilustroval R-kvadrát 1:

Problémy s R-na druhou
R-kvadrát přichází s inherentním problémem - další vstupní proměnné způsobí, že R-kvadrát zůstane stejný nebo se zvýší (je to způsobeno matematickým výpočtem R-kvadru). Proto i když další vstupní proměnné nevykazují žádný vztah s výstupními proměnnými, R-kvadrát se zvýší. Níže je uveden příklad, který vysvětluje takový výskyt.
Pochopení Upraveného R na druhou
Upravený R-kvadrát v zásadě zkoumá, zda k modelu přispívají další vstupní proměnné. Zvažte příklad použití dat shromážděných majitelem pizzy, jak je uvedeno níže:
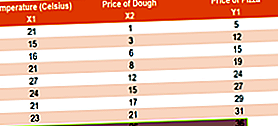
Předpokládejme, že majitel pizzy provede dvě regrese:
Regrese 1: Cena těsta (vstupní proměnná), Cena pizzy (výstupní proměnná)
Regrese 1 poskytuje R-kvadrát 0,9557 a upravený R-kvadrát 0,9493.
Regrese 2: Teplota (vstupní proměnná 1), Cena těsta (vstupní proměnná 2), Cena pizzy (výstupní proměnná)
Regrese 2 poskytuje R-kvadrát 0,9573 a upravený R-kvadrát 0,9431.
Ačkoli teplota by neměla vyvíjet žádnou prediktivní sílu na cenu pizzy, R-kvadrát se zvýšil z 0,9557 (regrese 1) na 0,9573 (regrese 2). Osoba může věřit, že regrese 2 má vyšší prediktivní sílu, protože R-kvadrát je vyšší. I když je vstupní proměnná teploty při předpovídání ceny pizzy zbytečná, zvýšila R-kvadrát. Tady vstupuje upravený R-kvadrát.
Upravený R-kvadrát zkoumá, zda k modelu přispívají další vstupní proměnné. Upravený R-kvadrát v Regrese 1 byl 0,9493 ve srovnání s upraveným R-kvadrátem v Regrese 2 0,9493. Upravený R-kvadrát je tedy schopen identifikovat, že vstupní proměnná teploty není užitečná při vysvětlování výstupní proměnné (cena pizzy). V takovém případě by upravený R-kvadrát ukazoval tvůrce modelu na použití Regrese 1 spíše než Regrese 2.
Příklad upraveného čtverce R.
Zvažte dva modely:
- Model 1 používá k předpovědi Y1 vstupní proměnné X1, X2 a X3.
- Model 2 používá vstupní proměnné X1 a X2 k předpovědi Y1.
Který model by měl být použit? Informace týkající se obou modelů jsou uvedeny níže:

Při srovnání R-kvadrát mezi Modelem 1 a Modelem 2 předpovídá R-kvadrát, že Model 1 je lepší model, protože přináší větší vysvětlující sílu (0,5923 v Modelu 1 oproti 0,5612 v Modelu 2).
Ve srovnání R-kvadrát mezi Modelem 1 a Modelem 2 upravený R-kvadrát předpovídá, že vstupní proměnná X3 přispívá k vysvětlení výstupní proměnné Y1 (0,4231 v modelu 1 vs. 0,3512 v modelu 2).
Jako takový by měl být použit Model 1, protože další vstupní proměnná X3 přispívá k vysvětlení výstupní proměnné Y1.
Dodatečné zdroje
Finance nabízí analytika pro finanční modelování a oceňování (FMVA) ™ Certifikace FMVA®. Připojte se k více než 350 600 studentům, kteří pracují pro společnosti jako Amazon, J.P. Morgan a certifikační program Ferrari pro ty, kteří chtějí posunout svou kariéru na další úroveň. Chcete-li se neustále učit a rozvíjet svou kariéru, budou užitečné následující finanční zdroje:
- Pojmy základní statistiky pro finance Pojmy základní statistiky pro finance Dobré pochopení statistik je zásadně důležité, aby nám pomohlo lépe porozumět financím. Statistické koncepty mohou navíc pomoci investorům sledovat
- Metoda vysoké a nízké vs. regresní analýza Metoda vysoké a nízké regresní analýzy Metoda vysoké a nízké regresní analýzy jsou dvě hlavní metody odhadu nákladů používané k odhadu výše fixních a variabilních nákladů. Manažeři obvykle musí rozdělit smíšené náklady na své fixní a variabilní složky, aby mohli předvídat a plánovat budoucnost.
- Nezávislá proměnná Nezávislá proměnná Nezávislá proměnná je vstup, předpoklad nebo ovladač, který je změněn za účelem posouzení jejího dopadu na závislou proměnnou (výsledek).
- Druhy finanční analýzy Druhy finanční analýzy Finanční analýza zahrnuje použití finančních údajů k vyhodnocení výkonnosti společnosti a doporučení, jak se může do budoucna zlepšit. Finanční analytici primárně provádějí svou práci v aplikaci Excel pomocí tabulky k analýze historických dat a vytváření projekcí Typy finanční analýzy