Efektivní roční úroková sazba (EAR) je úroková sazba, která je upravena pro složení složené míry růstu. Složená míra růstu je měřítkem používaným konkrétně v obchodních a investičních kontextech, které udává míru růstu za více časových období. Jedná se o měřítko neustálého růstu datové řady. Největší výhodou rychlosti složeného růstu je, že metrika bere v úvahu složený efekt. za dané období. Jednoduše řečeno, efektivní roční úroková sazba je úroková sazba. Úrokové výdaje Úrokové výdaje vznikají ze společnosti, která financuje prostřednictvím dluhu nebo kapitálového leasingu. Úroky se nacházejí ve výkazu zisku a ztráty, ale lze je vypočítat také pomocí dluhového plánu. Plán by měl nastínit všechny hlavní dluhy, které má společnost v rozvaze, a vypočítat úrok vynásobením toho, co může investor vydělat (nebo zaplatit) za rok po zohlednění složení.
EAR lze použít k vyhodnocení úroků splatných z půjčky nebo jakéhokoli dluhu nebo k vyhodnocení výnosů z investice, jako je certifikát se zaručenou investicí (GIC) nebo spořicí účet.
Efektivní roční úroková sazba je také známá jako efektivní úroková sazba (EIR), roční ekvivalentní sazba (AER) nebo efektivní sazba. Porovnejte to s roční procentní sazbou (RPSN) Roční procentní sazbou (RPSN) Roční procentní sazbou (RPSN) je roční úroková sazba, kterou musí jednotlivec zaplatit z půjčky nebo kterou obdrží na vkladovém účtu. RPSN je v konečném důsledku jednoduchý procentní termín používaný k vyjádření číselné částky vyplácené jednotlivcem nebo entitou ročně za privilegium půjčovat si peníze. který je založen na jednoduchém úroku Jednoduchý úrok Jednoduchý úrokový vzorec, definice a příklad. Jednoduchý úrok je výpočet úroku, který nebere v úvahu účinek složení. V mnoha případech se úrok spojuje s každým určeným obdobím půjčky, ale v případě jednoduchého úroku tomu tak není. Výpočet jednoduchého úroku se rovná částce jistiny vynásobené úrokovou sazbou vynásobené počtem období. .
Vzorec EAR je uveden níže:
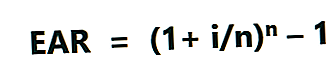
Kde:
- i = Uvedená roční úroková sazba
- n = Počet slučovacích období
Efektivní roční sazba na základě složení
Níže uvedená tabulka ukazuje rozdíl v efektivní roční sazbě, když se mění slučovací období.
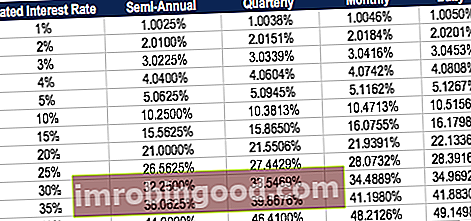
Tabulka: Kurz základů financí s pevným příjmem
Například EAR 1% stanovené úrokové sazby složené čtvrtletně je 1,0038%.
Důležitost efektivní roční sazby
Efektivní roční úroková sazba je důležitým nástrojem, který umožňuje hodnocení skutečné návratnosti investice nebo skutečné úrokové sazby z úvěru.
Uvedená roční úroková sazba a efektivní úroková sazba se mohou významně lišit v důsledku složení. Efektivní úroková sazba je důležitá při zjišťování nejlepší půjčky nebo při určování, která investice nabízí nejvyšší míru návratnosti. Vnitřní míra návratnosti (IRR) Vnitřní míra návratnosti (IRR) je diskontní sazba, díky níž je čistá současná hodnota (NPV) projektu nulová. Jinými slovy, jedná se o očekávanou složenou roční míru návratnosti, která se získá na projektu nebo investici.
V případě složení je EAR vždy vyšší než uvedená roční úroková sazba.
Příklad EAR
Předpokládejme například, že banka nabízí váš vklad ve výši 10 000 $ s úrokovou sazbou 12% uvedenou měsíčně. Níže uvedená tabulka ukazuje koncept efektivní roční úrokové sazby:
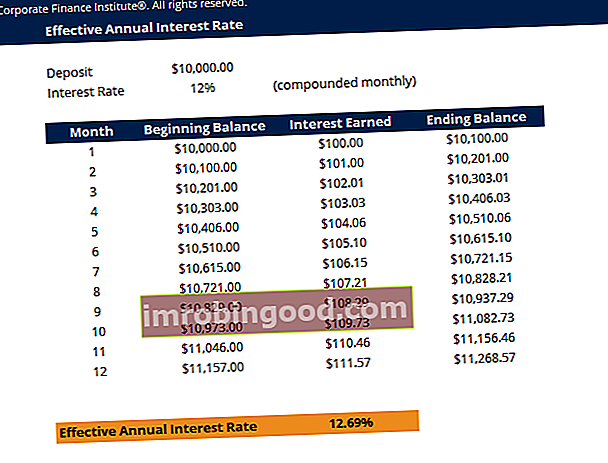Tabulka: Kurz základů financí s pevným příjmem
Úrok z 1. měsíce: Počáteční zůstatek (10 000 USD) x Úroková sazba (12% / 12 = 1%) = 100 USD
Úrok 2 měsíc: Počáteční zůstatek (10 100 $) x úroková sazba (12% / 12 = 1%) = 101 $
Změna v procentech z počátečního zůstatku (10 000 USD) na konečný zůstatek (11 268 USD) je (11 268 USD - 10 000 USD) / 10 000 USD = 0,12683 nebo 12,683%, což je efektivní roční úroková sazba. I když banka nabídla 12% uvedenou úrokovou sazbu, vaše peníze vzrostly o 12,683% kvůli měsíčnímu složení.
Efektivní roční úroková sazba vám umožňuje určit skutečnou návratnost investic (ROI) Vzorec návratnosti investic (ROI) Návratnost investic (ROI) je finanční poměr používaný k výpočtu výhody, kterou investor získá ve vztahu k jejich investičním nákladům. Nejčastěji se měří jako čistý příjem dělený původními kapitálovými náklady investice. Čím vyšší je poměr, tím větší je získaná výhoda. .
Stáhněte si šablonu zdarma
Zadejte své jméno a e-mail do níže uvedeného formuláře a stáhněte si bezplatnou šablonu zobrazenou výše!
Jak vypočítat efektivní úrokovou sazbu?
Chcete-li vypočítat efektivní úrokovou sazbu pomocí vzorce EAR, postupujte takto:
1. Určete uvedenou úrokovou sazbu
Uvedená úroková sazba (nazývaná také roční procentní sazba nebo nominální sazba) se obvykle nachází v titulcích smlouvy o půjčce nebo vkladu. Příklad: „Roční sazba 36%, úroky účtovány měsíčně.“
2. Určete počet slučovacích období
Složité období je obvykle měsíční nebo čtvrtletní. Složené období může být 12 (12 měsíců v roce) a 4 pro čtvrtletí (4 čtvrtletí v roce).
Pro vaši informaci:
- Měsíčně = 12 slučovacích období
- Čtvrtletně = 4 slučovací období
- Bi-Weekly = 26 slučovacích období
- Týdně = 52 slučovacích období
- Denně = 365 složených období
3. Použijte vzorec EAR: EAR = (1+ i / n) n - 1
Kde:
- i = Uvedená úroková sazba
- n = Složené období
Příklad
Výpočet efektivní roční úrokové sazby kreditní karty s roční sazbou 36% a úrokem účtovaným měsíčně:
1. Uvedená úroková sazba: 36%
2. Počet slučovacích období: 12
Proto EAR = (1 + 0,36 / 12) ^ 12 - 1 = 0,4257 nebo 42,57%.
Proč banky nepoužívají efektivní roční úrokovou sazbu?
Když banky účtují úrok, použije se místo efektivní roční úrokové sazby uvedená úroková sazba. Důvodem je, aby se spotřebitelé domnívali, že platí nižší úrokovou sazbu.
Například pro půjčku se stanovenou úrokovou sazbou 30%, složenou měsíčně, by efektivní roční úroková sazba byla 34,48%. Banky obvykle inzerují uvedenou úrokovou sazbu ve výši 30%, nikoli efektivní úrokovou sazbu ve výši 34,48%.
Když banky vyplácejí úroky na vašem vkladovém účtu, je EAR inzerována tak, aby vypadala atraktivněji než uvedená úroková sazba.
Například pro vklad se stanovenou sazbou 10% složenou měsíčně by efektivní roční úroková sazba byla 10,47%. Banky budou inzerovat efektivní roční úrokovou sazbu 10,47%, spíše než uvedenou úrokovou sazbu 10%.
V zásadě ukazují, která sazba se jeví jako příznivější.
Související čtení
Finance je globálním poskytovatelem kurzů finančního modelování a certifikace finančních analytiků Certifikace FMVA® Připojte se k více než 350 600 studentům, kteří pracují pro společnosti jako Amazon, J.P.Morgan a Ferrari. Chcete-li pokračovat v rozvoji své kariéry finančního profesionála, podívejte se na následující další finanční zdroje:
- Očekávaný výnos Očekávaný výnos Očekávaný výnos z investice je očekávaná hodnota rozdělení pravděpodobnosti možných výnosů, které může poskytnout investorům. Návratnost investice je neznámá proměnná, která má různé hodnoty spojené s různými pravděpodobnostmi.
- Základní body Základní body (BPS) Základní body (BPS) jsou běžně používanou metrikou pro měření změn úrokových sazeb. Základní bod je setina jednoho procenta. Viz příklady. Tato metrika
- Výnos z kapitálových výnosů Výnos z kapitálových výnosů Výnos zisků z kapitálu (CGY) je zhodnocení ceny investice nebo cenného papíru vyjádřené v procentech. Protože výpočet výnosu kapitálového zisku zahrnuje tržní cenu cenného papíru v čase, lze jej použít k analýze kolísání tržní ceny cenného papíru. Viz výpočet a příklad
- Vážené průměrné náklady na kapitál (WACC) WACC WACC jsou vážené průměrné náklady na kapitál společnosti a představují jejich smíšené náklady na kapitál včetně vlastního kapitálu a dluhu. Vzorec WACC je = (E / V x Re) + ((D / V x Rd) x (1-T)). Tato příručka poskytne přehled o tom, co to je, proč se používá, jak to vypočítat, a také poskytuje kalkulačku WACC ke stažení
