LASSO, zkratka pro Least Absolute Shrinkage and Selection Operator, je statistický vzorec, jehož hlavním účelem je výběr funkcí a regularizace datových modelů. Metodu poprvé představil v roce 1996 profesor statistiky Robert Tibshirani. LASSO zavádí parametry do součtu modelu a dává mu horní hranici, která funguje jako omezení součtu, aby zahrnoval absolutní parametry v povoleném rozsahu.
Metoda LASSO reguluje parametry modelu zmenšením regresních koeficientů a snížením některých z nich na nulu. Fáze výběru prvků nastává po smrštění, kde je pro použití v modelu vybrána každá nenulová hodnota. Tato metoda je významná při minimalizaci chyb predikce, které jsou běžné ve statistických modelech. Kvantitativní analýza Kvantitativní analýza je proces shromažďování a vyhodnocování měřitelných a ověřitelných údajů, jako jsou výnosy, podíl na trhu a mzdy, aby bylo možné pochopit chování a výkonnost podnikání. V éře datových technologií je kvantitativní analýza považována za preferovaný přístup k přijímání informovaných rozhodnutí. .
LASSO nabízí modely s vysokou přesností predikce. Přesnost se zvyšuje, protože metoda zahrnuje zmenšení koeficientů, což na oplátku snižuje rozptyl a minimalizuje zkreslení. Nejlépe funguje, když je nízký počet pozorování a vysoký počet funkcí. Silně spoléhá na parametr λ, který je řídícím faktorem smršťování. Čím větší je λ, tím více koeficientů je nuceno k nule.
Když se λ rovná nule, stane se model regresí Obyčejných nejmenších čtverců. V důsledku toho, když se λ zvyšuje, rozptyl se významně snižuje a zkreslení ve výsledku se také zvyšuje. Lasso je také užitečným nástrojem k eliminaci všech proměnných, které jsou irelevantní a které nesouvisí s proměnnou odezvy.
LASSO ve statistických lineárních modelech
Statistický model je matematická reprezentace problému v reálném životě. Model by měl problém vyjadřovat co nejblíže reálnému světu a zároveň by měl být jednoduchý a snadno pochopitelný. Model se skládá z vysvětlujících a odezvových proměnných.
The vysvětlující proměnná je nezávislá proměnná, která je na uvážení výzkumného pracovníka. Nezávislé proměnné jsou vstupy do modelu, které lze výzkumníkem měřit za účelem stanovení jejich vlivu na výsledky modelu.
The proměnná odezvy je závislá proměnná Závislá proměnná Závislá proměnná je proměnná, která se bude měnit v závislosti na hodnotě jiné proměnné, která se nazývá nezávislá proměnná. který tvoří hlavní zaměření experimentu. Tvoří výsledek experimentu, kterým může být jediný výsledek v případě jednorozměrných modelů, nebo v případě vícerozměrných modelů více výsledků.
LASSO je nedílnou součástí procesu vytváření modelu, zejména s využitím výběru funkcí. Fáze výběru funkcí pomáhá při výběru vysvětlujících proměnných, které jsou nezávislými proměnnými, a tedy vstupními proměnnými v modelu.
Vstupní proměnné jsou důležité prvky, které určují výstup modelu a které pomáhají při měření jejich vlivu na proměnné odezvy. Výběr správných proměnných určuje přesnost modelu. Fáze výběru funkcí LASSO pomáhá při správném výběru proměnných.
Odhad pomocí LASSO
Statistické modely spoléhají na LASSO pro přesný výběr proměnných a regularizaci. V lineární regresi Regresní analýza Regresní analýza je sada statistických metod používaných pro odhad vztahů mezi závislou proměnnou a jednou nebo více nezávislými proměnnými. Lze jej použít k posouzení síly vztahu mezi proměnnými a k modelování budoucího vztahu mezi nimi. například LASSO zavádí horní mez pro součet čtverců, čímž minimalizuje chyby přítomné v modelu. Odhadovač LASSO závisí na parametru λ.
Parametr λ řídí sílu smrštění, kde zvýšení λ má za následek zvýšení smrštění. Horní mez součtu všech koeficientů je nepřímo úměrná parametru λ. Když horní mez zvyšuje hodnotu, parametr λ klesá. Když horní mez klesá, současně se zvyšuje parametr λ.
Jak se horní hranice zvyšuje směrem k nekonečnu, parametr λ se blíží nule, a proto převádí experiment na Obyčejné nejmenší čtverce, kde je parametr λ vždy roven nule. Když se horní mezní koeficienty přiblíží k nule, hodnota parametru λ se zvýší směrem k nekonečnu.
Geometrie LASSO
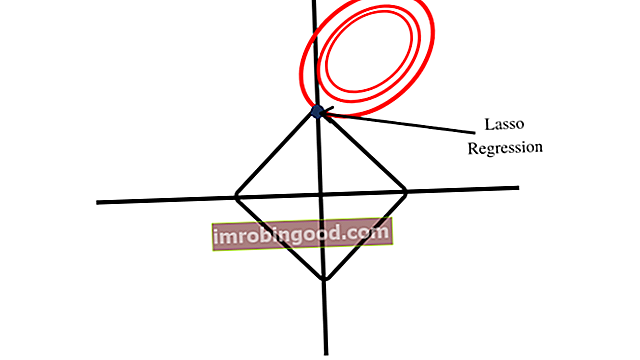
LASSO vytvoří na ploše pro svou oblast omezení tvar kosočtverce, jak je znázorněno na obrázku níže. Tvar kosočtverce zahrnuje rohy, na rozdíl od kruhového tvaru vytvořeného hřebenovou regresí. Blízkost prvního bodu k rohu ukazuje, že model má jeden koeficient, který se rovná nule.
Oblast omezení hřebenové regrese tvoří kruhový tvar, který při vykreslení neobsahuje žádné rohy podobné těm, které jsou tvořeny oblastí omezení LASSO. Kožešinové regresní koeficienty se proto nemohou rovnat nule.
Vážené LASSO
Vážené LASSO je výsledkem výzkumného pracovníka, který izolovaně postihuje regresní koeficienty. To znamená, že namísto penalizace společného parametru λ na všechny koeficienty jsou koeficienty penalizovány jednotlivě s použitím různých parametrů.
Váhy lze určit pomocí algoritmu LASSO k přiřazení závaží vhodným způsobem pro přesné modelování. Podobným vážením regresních koeficientů je kooperativní LASSO, kde jsou koeficienty penalizovány ve skupinách, které jsou považovány za podobné.
Dodatečné zdroje
Finance je oficiálním poskytovatelem Certified Banking & Credit Analyst (CBCA) ™ Certifikace CBCA ™ Certifikace Certified Banking & Credit Analyst (CBCA) ™ je celosvětovým standardem pro úvěrové analytiky, který zahrnuje finance, účetnictví, kreditní analýzu, analýzu peněžních toků, modelování smluv, splácení půjček atd. certifikační program, jehož cílem je transformovat kohokoli na špičkového finančního analytika.
Abychom se dál učili a rozvíjeli své znalosti finanční analýzy, velmi doporučujeme další finanční zdroje uvedené níže:
- Metody předpovědi Metody předpovědi Nejlepší metody předpovědi. V tomto článku vysvětlíme čtyři typy metod předpovídání výnosů, které finanční analytici používají k předpovídání budoucích výnosů.
- Nezávislá proměnná Nezávislá proměnná Nezávislá proměnná je vstup, předpoklad nebo ovladač, který je změněn za účelem posouzení jejího dopadu na závislou proměnnou (výsledek).
- Vícenásobná lineární regrese Vícenásobná lineární regrese Vícenásobná lineární regrese označuje statistickou techniku používanou k předpovědi výsledku závislé proměnné na základě hodnoty nezávislých proměnných
- Analýza scénářů Analýza scénářů Analýza scénářů je technika používaná k analýze rozhodnutí spekulací různých možných výsledků finančních investic. Ve finančním modelování to

